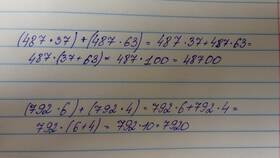В математике противоположные числа обладают особой характеристикой, которая определяет результат их сложения. Это фундаментальное свойство играет важную роль в алгебре и арифметике.
Содержание
В математике противоположные числа обладают особой характеристикой, которая определяет результат их сложения. Это фундаментальное свойство играет важную роль в алгебре и арифметике.
Определение противоположных чисел
Противоположные числа - это два числа, отличающиеся только знаком. Для любого числа a существует противоположное ему число -a.
- Примеры пар противоположных чисел: 5 и -5, -3 и 3, 0 и 0
- На числовой прямой противоположные числа расположены симметрично относительно нуля
- Модули противоположных чисел равны
Сумма противоположных чисел
| Первое число | Второе число | Сумма |
| 7 | -7 | 0 |
| -4.5 | 4.5 | 0 |
| 0 | 0 | 0 |
Математическое доказательство
Сумма любого числа и ему противоположного всегда равна нулю:
a + (-a) = 0
Это следует из:
- Свойства сложения с нулем: a + 0 = a
- Определения противоположного числа: a + (-a) = 0
- Коммутативности сложения: -a + a = 0
Практическое применение
- Решение уравнений (перенос слагаемых через знак равенства)
- Упрощение алгебраических выражений
- Балансировка финансовых операций (доходы и расходы)
- Физические расчеты (равнодействующая противоположных сил)
Особый случай - ноль
Число 0 является противоположным самому себе, что подтверждается равенством: 0 + 0 = 0. Это единственное число с таким свойством в математике.
